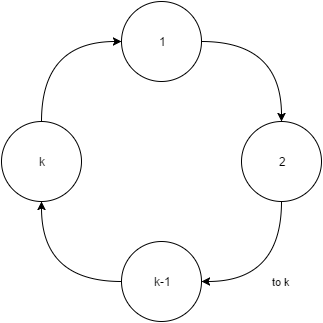
Proof of optimality (by induction):
RTP: For n-number of nodes the algorithm has O(n) maximum communication steps.
For n=1: There are 0 communication steps.
For n=2: There is 1 communication step.
For n=k: There are k communication steps.
For n=k+1: There is 1 communication step.
∴ The number of communication steps can never exceed the number of nodes in this configuration, i.e. This is the optimal broadcast algorithm for this network design. The smallest number of communication steps is 1 (between more than one node) and the largest possible amount of steps is k.
This is a simple example of an algorithmic proof of optimality. For parallel systems and more complex network structure the proofs can become more involved.
